No Products in the Cart
The dichte eines gases, or gas density, is a surprisingly dynamic property. It tells us how much "stuff"—or mass—is packed into a certain amount of space, or volume. This isn't a static number like it is for a solid block of steel; for a gas, it changes dramatically with pressure and temperature, which is why it's such a crucial concept in fields like cryogenics.
Think about packing a suitcase. You could stuff it full of fluffy pillows. They don't weigh much, but they take up a ton of space. That's a good picture of a gas with low density—its molecules are spread out, not packed in tightly.

Now, imagine taking those pillows out and replacing them with a heavy stack of books. They're dense and compact, fitting a lot of mass into a small area. This represents a gas with high density, where the molecules are crammed closely together. Grasping this simple idea is the first step to understanding how gases behave under different conditions.
Unlike solids or liquids, you can't just look up a single density value for a gas. It's incredibly sensitive to its surroundings. Three main factors are always at play:
This interplay is what makes gas density so vital in cryogenics. When we cool nitrogen gas down to its liquid state at a frigid -196°C, its density skyrockets—by a factor of nearly 700.
This huge change in density is the very principle that makes cryogenic liquids such powerful tools. It allows an enormous amount of material to be stored in a relatively small, manageable volume inside highly engineered vessels.
In any lab, biobank, or industrial setting using cryogenics, getting a handle on gas density is a matter of both safety and efficiency. For instance, knowing the precise density of liquid nitrogen is how you calculate how much you actually have in your storage freezers and transport dewars.
It's also a critical safety concern. If a dense cryogenic liquid leaks and turns back into a gas in an enclosed room, it can rapidly push out all the breathable oxygen, creating a serious asphyxiation hazard. This is why every piece of cryogenic equipment, from the storage vessels to the safety sensors, is engineered with these physical principles in mind. It's all about managing the dichte eines gases safely, protecting both your valuable samples and your team.
If you need to figure out the dichte eines gases (gas density), you don’t have to start in a high-tech lab. The journey begins with a cornerstone of physics and chemistry: the Ideal Gas Law. This surprisingly simple formula is the best place to start for estimating gas density under most everyday conditions, giving us a solid baseline for nearly any calculation.

You probably remember the classic version, PV = nRT. For our purposes, though, we can rearrange it into a much more useful form for finding density (represented by the symbol ρ).
ρ = PM / RT
It might look a bit complex at first glance, but think of it as a recipe with just four main ingredients. Once you get a feel for what each part does, you can confidently predict how gases will behave in your facility.
Each letter in that density formula stands for a specific physical property. When you slot in the correct values for your situation, the gas density almost calculates itself. Let's take a closer look at each component.
Getting a feel for how these variables interact is key. Right away, you can see why chilling a gas (lowering T) makes it so much denser—a foundational concept in cryogenics. You can take a deeper dive into the extreme cold of liquid nitrogen and its properties in our detailed article here.
Let's make this real. We'll calculate the density of nitrogen gas (N₂) under what's known as Standard Temperature and Pressure (STP), a common benchmark in science and industry.
First, we need to line up our ingredients for nitrogen:
Now, we just pop these values into our formula:
ρ = (101,325 Pa * 0.02802 kg/mol) / (8.314 J/(mol·K) * 273.15 K)
Run the numbers, and you get:
ρ ≈ 1.25 kg/m³
What does this mean? It tells us that at standard conditions, a cubic metre of nitrogen gas has a mass of about 1.25 kilograms. This isn't just a number; it's a hugely valuable piece of information for everything from designing ventilation systems to making initial volume-to-mass conversions.
The Ideal Gas Law is a fantastic tool. It gives us a reliable starting point for estimating the dichte eines gases by working on a simple, clean set of assumptions: gas particles are tiny, dimensionless points that zip around without ever interacting. For many standard applications, this model works remarkably well. But what happens when conditions get extreme, like in the world of cryogenics?
Under the intense pressures and frigid temperatures needed to liquefy gases, this neat and tidy model begins to fall apart. The assumptions that hold true in a warm, low-pressure room just don't reflect reality anymore. It turns out that real gas molecules aren't just points; they have actual volume, and they definitely interact with each other.
Think of it like a large, empty ballroom. A few people scattered across the floor can move freely without ever bumping into each other—that’s our ideal gas. Now, picture that same ballroom packed shoulder-to-shoulder for a concert. People can't ignore their neighbours; they take up space and constantly jostle for position. This crowded room is a much better analogy for a real gas under high pressure.
When we really push gases to their limits, two key factors that the ideal model conveniently ignores become impossible to overlook. These are the very reasons our calculations need a reality check.
These two effects pull in opposite directions. Getting a handle on their delicate balance is crucial for accurately predicting the dichte eines gases in demanding cryogenic applications.
To account for these real-world behaviours, scientists developed more sophisticated models. The most famous of these is the Van der Waals equation. It essentially looks like a souped-up version of the ideal gas law, adding specific correction factors to account for both molecular volume and those pesky intermolecular forces.
This isn't just an academic exercise; it has profound real-world consequences. Take the recent energy situation in Germany, for example. In 2022, natural gas consumption dropped by a staggering 14% compared to the 2018-2021 average, a direct result of pipeline disruptions. Managing this shift required a deep understanding of gas density, as the low density of natural gas (around 0.7-0.8 kg/m³) makes its storage and transport a massive logistical challenge. You can read more about these gas consumption trends and their impact on the German Federal Network Agency website.
For cryogenic specialists, this just underscores why precise density management is non-negotiable. Storing liquefied gases like nitrogen, with its liquid density of approximately 0.808 g/cm³ at -196°C, relies on equipment engineered to handle these real-gas effects perfectly.
This is exactly why high-quality, purpose-built cryogenic vessels are so critical. When you're liquefying nitrogen or argon, you are operating far, far outside the "ideal" range. Equipment like the AC LAC XL/3XL series from Auguste Cryogenics is designed from the ground up to manage these real-gas behaviours, ensuring the integrity of stored biological samples by maintaining ultra-low evaporation rates. The transition from gas to liquid is where ideal models completely fail, and only engineering grounded in real-gas physics can ensure safety and efficiency. Without accounting for molecular volume and attraction, trying to predict fill levels, manage pressure build-up, and ensure safe transport would be nothing more than guesswork.
Theory is one thing, but putting it into practice is where real understanding clicks. Let's move from abstract concepts to concrete calculations, working through the dichte eines gases for three of the most important cryogenic gases: nitrogen (N₂), oxygen (O₂), and argon (Ar). This hands-on approach will show you exactly how to determine their density under different, very real conditions.
We're going to tackle two key scenarios for each gas. First, we’ll calculate its density at Standard Temperature and Pressure (STP) using the Ideal Gas Law—it's a great baseline. Then, we'll shift to cryogenic conditions to see just how much real-gas behaviour changes the game. For anyone managing cryogenic materials day-to-day, this is an invaluable exercise.
This diagram offers a fantastic visual breakdown, contrasting the neat, orderly assumptions of ideal gases with the far more complex reality of how real gas molecules behave under pressure.
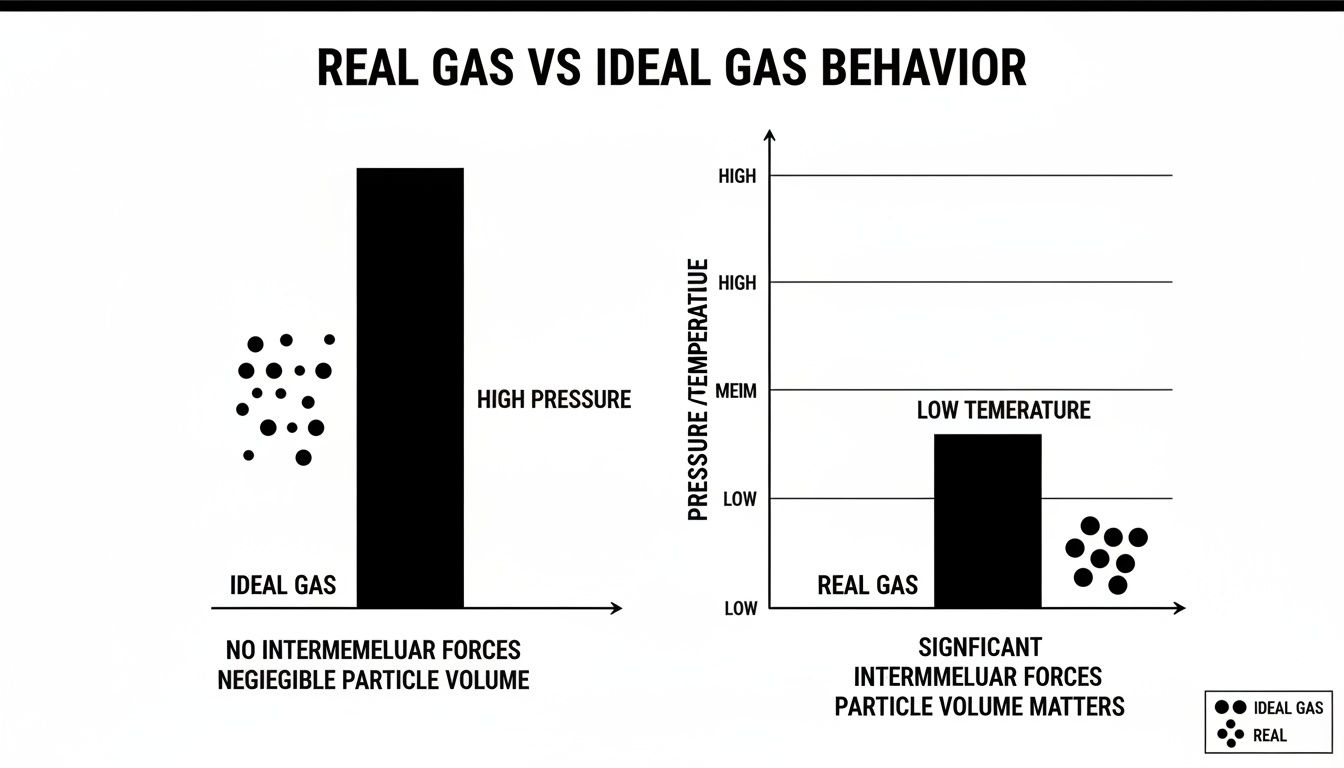
You can see how real gas particles actually take up space and attract each other. This is a critical detail the ideal gas model completely ignores, and it makes a massive difference in cryogenic applications.
Nitrogen is the undisputed workhorse of the cryogenics world. Let's pin down its density under standard conditions before we look at what happens when it becomes a liquid.
Scenario A: Ideal Gas Density at STP
We'll use our trusty formula: ρ = PM / RT.
Plugging those values in gives us:
ρ = (101,325 Pa * 0.028014 kg/mol) / (8.314 J/(mol·K) * 273.15 K) ≈ 1.25 kg/m³
So, under normal atmospheric conditions, a cubic metre of nitrogen gas weighs about 1.25 kilograms.
Scenario B: Real-World Liquid Density
Now for the interesting part. Let's look at liquid nitrogen (LIN) at its boiling point of -195.8°C (77.35 K). At this temperature, the molecules are packed together so tightly that the Ideal Gas Law becomes useless. We have to rely on measured, experimental values.
The measured density of liquid nitrogen is a staggering 808 kg/m³.
Take a moment to appreciate that difference. Liquid nitrogen is over 646 times denser than its gaseous form at STP. This incredible density increase is the very reason cryogenic liquids are such powerful and efficient ways to store and transport gases.
Oxygen is absolutely essential for countless medical and industrial processes, making its density a critical parameter. If you're curious about its other unique properties, you can explore our guide on the characteristics of oxygen.
Scenario A: Ideal Gas Density at STP
Once again, we turn to ρ = PM / RT.
Let's run the numbers:
ρ = (101,325 Pa * 0.031998 kg/mol) / (8.314 J/(mol·K) * 273.15 K) ≈ 1.43 kg/m³
As we'd expect from its higher molar mass, oxygen gas is a bit denser than nitrogen gas.
Scenario B: Real-World Liquid Density
For liquid oxygen (LOX) at its boiling point of -183°C (90.15 K), we again have to use measured data.
The measured density of liquid oxygen is approximately 1,141 kg/m³. That's right—LOX is significantly denser than water.
As an inert gas, argon is indispensable for specialised welding and sensitive lab work. Let's see how its density stacks up.
Scenario A: Ideal Gas Density at STP
You know the drill: ρ = PM / RT.
And the result:
ρ = (101,325 Pa * 0.039948 kg/mol) / (8.314 J/(mol·K) * 273.15 K) ≈ 1.78 kg/m³
Being the heaviest of the three gases we've looked at, argon is also the densest at STP, just as we'd predict.
Scenario B: Real-World Liquid Density
Finally, for liquid argon (LAr) at its boiling point of -185.8°C (87.35 K), the measured density is what matters.
The measured density of liquid argon is approximately 1,395 kg/m³.
These examples couldn't make it clearer: there's a world of difference between theoretical gas calculations and the physical reality of cryogenic liquids.
This table really brings home the point. It contrasts the "ideal" density we calculated for these gases at standard temperature and pressure with their actual, measured liquid densities. The difference is enormous.
| Gas | Molar Mass (g/mol) | Ideal Gas Density at STP (kg/m³) | Liquid Density at Boiling Point (kg/m³) | Density Increase Factor |
|---|---|---|---|---|
| **Nitrogen (N₂) ** | 28.014 | 1.25 | 808 | ~646x |
| **Oxygen (O₂) ** | 31.998 | 1.43 | 1,141 | ~798x |
| **Argon (Ar) ** | 39.948 | 1.78 | 1,395 | ~784x |
Looking at the "Density Increase Factor" column, you can see why liquefaction is so fundamental to cryogenics. You are compressing an incredible amount of material into a very small volume, which is the key to efficient storage and transport.
While calculations give us a strong theoretical grasp, in any real-world lab or industrial facility, you need direct, real-time measurements. Moving from the formula to the field means relying on specialised instruments built for accuracy and reliability. These tools eliminate the guesswork and provide the hard data needed for safety, efficiency, and compliance—especially when you’re dealing with valuable cryogenic materials.

Simply put, you can’t manage what you don’t measure. In cryogenics, where conditions are extreme, theoretical values alone just don’t cut it. Precise, continuous monitoring is absolutely essential for everything from inventory control to preventing dangerous over-pressurisation events.
Choosing the right instrument depends entirely on your application. A biotech lab handling high-purity medical gases has very different needs from an industrial plant monitoring bulk gas transport. Three primary types of instruments tend to lead the pack.
Modern cryogenic vessels, like those we supply at Cryonos GmbH, often come with advanced inventory systems that provide this critical data automatically. These integrated sensors do away with the need for manual, error-prone measurements, offering a constant, real-time view of gas levels and density.
This shift towards automated monitoring is not just about convenience; it's a fundamental improvement in safety and operational efficiency. It ensures that biobanks, labs, and industrial users have the precise data they need to stay compliant and protect their assets.
The logistical challenges of managing gases are significant, particularly in economies with high demand. For instance, the density of industrial gases like nitrogen has a parallel in Germany's natural gas sector. Consumption there hit 94.34 billion cubic meters back in 2001, a figure that reflects immense storage and transport demands. This reliance is starkly highlighted by a daily import deficit of 2.535 trillion cubic feet.
When consumption dropped 14% in 2022 following pipeline disruptions, it only amplified the need for efficient gas handling solutions—a pressure felt across all industries. You can find more insights on Germany's energy statistics at IndexMundi.
This is precisely why state-of-the-art solutions like AC Micro Bulk systems are engineered with reliability front and centre, offering minimal evaporation rates of less than 0.5% and long-term warranties. These systems provide the robust, real-world data needed to navigate a demanding operational landscape.
When you're working with cryogenic liquids, understanding gas density stops being a theoretical exercise and becomes an absolute necessity for staying safe. The most dramatic—and potentially dangerous—property of these super-cold liquids is their incredible expansion ratio when they turn back into a gas. This single physical principle is the root cause of the biggest risks in cryogenic handling.
Take liquid nitrogen, a workhorse in modern labs and biobanks. When just one litre of this frigid liquid warms up and vaporises, it doesn't just create one litre of gas. It expands to occupy nearly 700 litres of space. This isn't a small change; it's a massive, sudden increase in volume that can have explosive results if it's not managed correctly.
This huge expansion is the number one cause of over-pressurisation accidents. If a cryogenic liquid is sealed inside a container without a proper pressure relief system, the vaporising liquid will build up pressure with terrifying force. As the temperature ticks up, the pressure can rapidly overpower the structural limits of the vessel, leading to a catastrophic failure.
This is exactly why medically-licensed cryogenic freezers and transport vessels are engineered with multiple, redundant safety-relief valves and burst discs. These aren't optional extras; they are essential systems designed to safely vent the expanding gas and prevent a disastrous rupture.
This design principle ensures that the immense pressure generated during normal evaporation or accidental warming is handled automatically. It's what protects both your team and the priceless materials you have stored inside. Without these safeguards, every cryogenic dewar would essentially be a ticking time bomb.
Beyond the risk of explosion, gas density introduces another, more subtle danger: asphyxiation. Most common cryogenic gases, like nitrogen and argon, are heavier than the air we breathe. If a major leak happens in a poorly ventilated room, this cold, dense gas won’t simply rise and float away. Instead, it will sink and pool at floor level, silently pushing out the life-sustaining oxygen.
This creates an oxygen-deficient atmosphere that can lead to unconsciousness in just a couple of breaths, often with no warning signs like choking or gasping. For a deeper dive into safe handling practices, our guide on the 7 important rules for safe work with cryogenic liquids is a must-read.
Proper ventilation systems, oxygen monitoring alarms, and strict handling protocols are all direct responses to the physical reality of gas density. Every safety procedure is built on the foundation of managing these predictable physical behaviours. It is this deep understanding that allows for the safe, routine use of these powerful materials, giving you operational excellence and peace of mind.
Let's pull all these ideas together and look at how they play out in the real world. Here are some of the most common questions we hear from people working in labs, biobanks, and industrial facilities every day.
This is a big one, and it's easy to overlook. When you go up in altitude, there's less atmosphere pressing down on you. That means the atmospheric pressure drops.
This change directly impacts the dichte eines gases (gas density). With less pressure squishing them together, gas molecules have more room to spread out. The result? Gas density goes down as altitude goes up. For any lab or facility located high above sea level, this isn't just a trivial fact—it's a critical operational variable. You'll need to recalibrate sensitive instruments and tweak your storage calculations to account for the thinner air.
It's a common point of confusion: why doesn't Liquefied Natural Gas (LNG) have one standard density? The answer is that LNG isn't one single, pure substance. It's a blend.
While methane is the main component, LNG also contains different amounts of ethane, propane, and butane. The exact recipe changes from one batch to another, and that's what determines its final density.
For energy suppliers, this variation is a massive deal. The density of LNG is directly linked to its energy content. Nailing down the precise value is essential for accurate billing and managing the complex logistics of transport and storage.
Simply put, a denser batch of LNG with more ethane and propane packs a bigger energy punch per cubic metre than a batch that's almost pure methane.
You'll often hear the term relative density, particularly during safety briefings. It’s a bit different from the absolute density we've been talking about (which is measured in units like kg/m³). Relative density is just a straightforward, unitless comparison.
It tells you how dense a gas is compared to a reference gas—and that reference is almost always the air around us.
Its main job is to help with quick safety assessments. If you have a leak, knowing the relative density tells you exactly how that gas is going to behave. Will it float up to the ceiling or sink to the floor? This is vital information that dictates where to place gas detectors and how to design ventilation systems to stop dangerous pockets of gas from building up.
For state-of-the-art cryogenic solutions designed with a deep understanding of gas physics, trust Cryonos GmbH. Explore our medically-licensed freezers and transport vessels engineered for maximum safety and efficiency at https://www.cryonos.shop.